Lithium Quantum Gas Microscope
Probing strong correlations physics in the Fermi Hubbard model
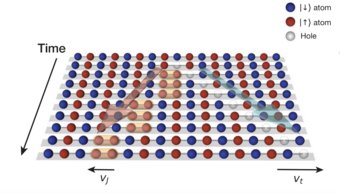
At the Lithium lab, we perform quantum simulation experiments with single-site and single-spin resolution. We load a deeply degenerate, two-component Fermi gas of 6Li in a single layer of a three-dimensional optical lattice and image it using a high-resolution objective. With this quantum gas microscope, we study the rich phases of the Fermi Hubbard model in one or two spatial dimensions.
Our overarching goal is to unravel the interplay of antiferromagnetic spin alignment and charge (density) propagation in strongly correlated systems. Past projects include the realization of antiferromagnetic correlations in a Fermi Hubbard gas, the detailed study of spin-density correlations, the observation of spin-charge separation in one dimension, and the direct imaging of magnetic Polarons in two dimensions.
Projects
Antiferromagnetic Spins

Fermionic atoms in a Mott insulator like to align antiferromagnetically at low temperatures. In one of our first projects, we demonstrated this behaviour by forming one-dimensional spin chains in the optical lattice. We can detect the spin orientation by pushing spins with a magnetic gradient in our superlattice before taking a single-atom-resolved image. See our publication "Spin- and density-resolved microscopy of antiferromagnetic correlations in Fermi-Hubbard chains" for details.
Spins and Holes in One Dimension
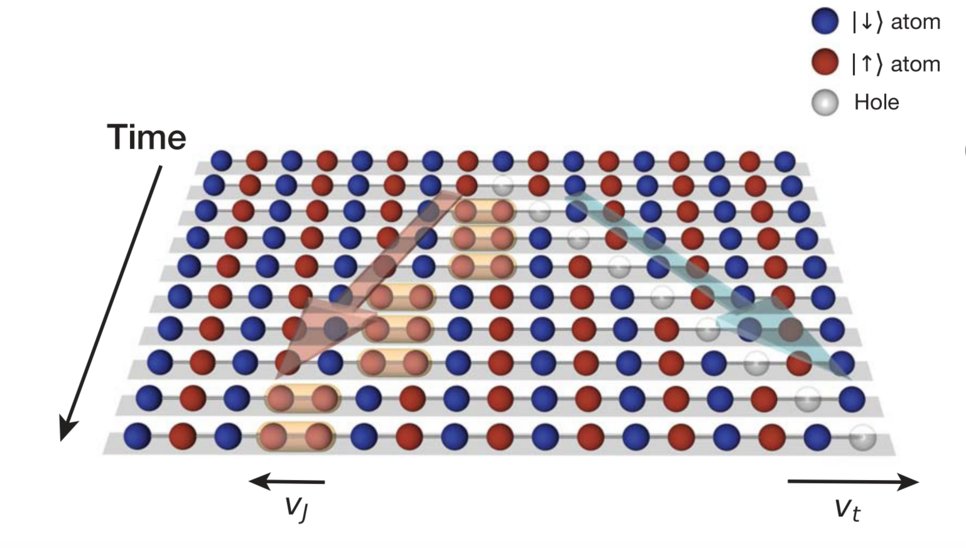
Particles show special behaviour when they can only move in one dimension. In a series of experiments, we probed the interplay of spins and holes and directly observed spin-charge separation, i.e. how an excitation due to a kicked-out atom splits up into a propagating density and spin excitation, which each move with different speeds. In an analysis of the relative distribution of all spins around the holes, we demonstrated how this is related to magnetic string correlations and incommensurate magnetism in these chains. Our results are summarized in the papers "Revealing hidden antiferromagnetic correlations in doped Hubbard chains via string correlators", "Direct observation of incommensurate magnetism in Hubbard chains", and "Time-resolved observation of spin-charge deconfinement in fermionic Hubbard chains".
Magnetic Polarons in Two Dimensions

Contrary to 1D, a hole in two dimensions can no longer propagate easily in a background of antiferromagnetic spins. Its motion locally changes the spin alignment and hole plus the surrounding spins form a new object: the polaron. With our microscope, we were able to image this magnetic cloud around individual mobile holes resolving how each correlation bond is affected by the nearby hole. See our paper "Imaging magnetic polarons in the doped Fermi-Hubbard model" with all the results.
The polaronic metal formed at low dopings has fundamentally different properties to a normal Fermi metal found at large hole doping. We carefully mapped out the transition between the two metallic phases and measured spin-spin, spin-hole-spin, and spin-spin-hole-hole correlations revealing the microscopics of the change.
Pairing of Holes
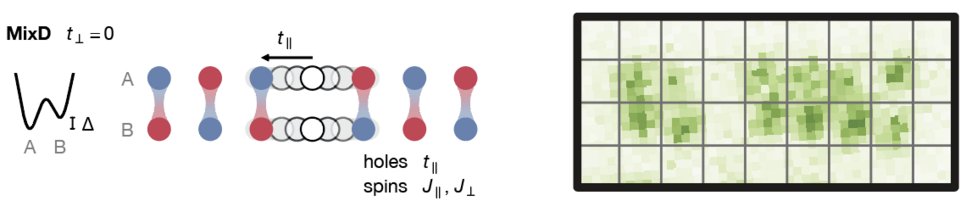
But what happens in detail when you dope a two-dimensional antiferromagnet with more than one hole? How do those polarons that form interact with each other? Can they bind into pairs or stripes and how is this mediated by the AFM background? When do the holes form a d-wave superconductor? Those are some of the fundamental questions of strongly correlated fermions. Recently, we directly saw the binding of holes in mixed-dimensional ladder systems. Here, the magnetic energy dominates over the kinetic energy of individual holes and pairs are formed, which can propagate without disturbing the magnetic background. Have a look at our paper “Magnetically mediated hole pairing in fermionic ladders of ultracold atoms”, which just got accepted in Nature.
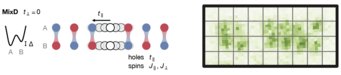
SPT Phase in a 2-leg ladder
Ladders systems with two connected legs are very interesting platforms that can display topological physics. We studied spin-1/2 ladders which are in the same phase as spin-1 chains. They thus show the same topological features (hidden order and edge states) as the famous Haldane phase. In our experiment, we realized a finite-size version with sufficiently low total entropy to directly measure these effects. Going beyond the spin model, we could show that the phase remains stable to strong density fluctuations. Check our Nature publication “Realizing the symmetry-protected Haldane phase in Fermi-Hubbard ladders”.
Experimental setup
We heat a small block of the fermionic Lithium-6 isotope to about 350 degree Celsius in an oven, generating an atomic beam out of a small aperture. A standard decreasing-field Zeeman slower decelerates the atoms, and a Magneto-Optical Trap (MOT) operating at 671 nm captures them in a steel octagon chamber. At this stage, we end up with about 109 atoms at a temperature of about 300 μK. Next, a second MOT is switched on operating near the narrow 2S1/2 ↔ 3P3/2 transition at 323 nm. After this UV cooling stage, we have ~5·108 atoms at roughly 70 μK. The UV light is provided by a home-built laser system using two nonlinear frequency conversions. The UV MOT enables the direct loading of an optical dipole trap at a magic wavelength close to 1070 nm. Using a large-volume high-power dipole trap we capture up to 10 million cold atoms from the UV MOT. A second, more tightly focused dipole trap at 1064nm is switched on afterwards to transport the atoms from the MOT chamber into the main glass cell. Above the microscope objective, we perform an efficient evaporative cooling to degeneracy in a Feshbach field.
Optical lattice generation and imaging
A superlattice is the superposition of two lattices with lattice constants that differ by a factor of two. They allow for flexible parallel manipulation of all atoms. To achieve superlattices with lattice constants >1 μm, we interfere pairs of phase-coherent laser beams under small angles.
After the evaporation, we first load the degenerate sample into a single vertical plane of a simple lattice. Then, we carefully ramp up the power of the other lattice beams.
Finally, the imaging is performed by Raman sideband cooling in a deep lattice, which pins the atoms while we collect fluorescent light on a camera. In this process, the spin information is quickly lost. But we developed a local Stern-Gerlach splitting, which allows us to convert the spin of each atom to a spatial position before imaging. We, thus, take snapshots of a quantum many-body system that include all orders of spatial density- and spin-z - correlations.
Selected Recent Publications
Research Group Members
- +49 89 32905-713 (Office) // -275 (Lab)
- +49 89 3 29 05 - 238 (MPQ)
- +49 89 32905-626
- +49 89 3 29 05 - 514 (Office) // - 275 (Lab)
- +49 89 3 29 05 -713 (Office) // -275 (Lab)
- +49 89 32905-215 (Office) // -275 (Lab)
- +49 89 3 29 05 - 713 (Office) // -275 (Lab)