A detailed look into the 2D SU(N) Fermi-Hubbard Model

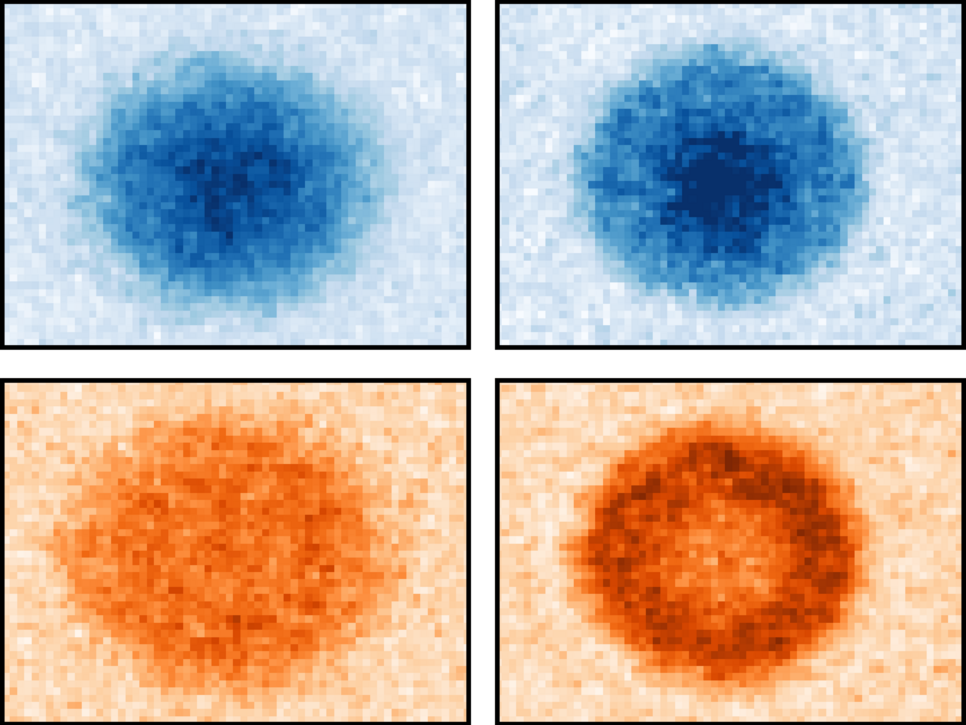
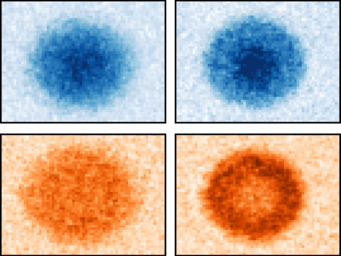
One of the important elements at the core of physics is the symmetry of a physical system. This can be a classical "left-right"-symmetry that we all know from everyday life, but also a symmetry that is expressed in other, more unusual properties. On fundamentally "quantum" property is the quantum "spin", which describes a kind of internal rotation of an object which only exists in quantum mechanics. Most quantum objects have this property, with the electron famously being a two-state spin system, which knows only "left" and "right" as possible values. While the electron spin is indeed accordingly associated with a two-fold "left-right" symmetry in the spin (specifically the so-called SU(2) symmetry), objects with different spin values typically are not symmetric, which means that the various possible orientations have different properties. This has particularly profound consequences in many-body systems of many particles with spin, as they interact to find the most optimal arrangement of positions and rotations among themselves. The new work explores the properties of the Fermi-Hubbard Model (FHM) in a two-dimensional (2D) optical lattice, invented for calculating the behaviors of electrons in complex materials, but with the additional twist of using atoms with a spin that has a large value and additionally conserves the a symmetry of higher order up to SU(6). For this, ytterbium atoms were used, cooled to near absolute zero, arranged in a light-created lattice that mimics the periodic potential experienced by electrons in solid materials. One powerful option provided by this setup is the manipulation of interaction strength and the introduction of spin-state variability (the "N" in SU(N) symmetry) to explore the macroscopic properties described by the "equation of state" (EoS) across different regimes, from metallic to Mott insulating phases. The study not only probes the density and site occupation probabilities but also introduces a method for in situ thermometry, enabling temperature measurements within the lattice without disturbing the system significantly. This approach is pivotal for understanding the thermodynamics and phase transitions within the model. The findings offer insights into the behavior of strongly correlated electron systems and their more complex cousins with higher symmetries and the fundamental processes that drive phenomena like magnetism. By comparing experimental results with new state-of-the-art numerical simulations, the research both provides a test of theoretical models and enhances our understanding of quantum phase transitions and the role of fluctuations in these systems.This work advances the field of quantum simulation by employing ultracold atom systems in investigating complex quantum phenomena that are particularly hard to describe purely by theoretical calculations, offering the potential to uncover new physical mechanisms and guiding the development of materials with novel electronic properties.

To read the full article, please visit Physical Review Letters.

See also Synopsis at physics.ap.org: A General Equation of State for a Quantum Simulator.