Negative Absolute Temperatures

Here we provide some answers to frequently asked questions on the intriguing topic of negative absolute temperatures.

Here we want to answer some frequently asked questions concerning negative absolute temperatures. If your question is not answered yet, please send an email to Simon Braun or Ulrich Schneider and we will add it.

What is absolute temperature?

Absolute temperature refers to temperature on the Kelvin scale, where 0K is the absolute zero point, where all motion in a classical gas would stop.

Can all systems achieve negative temperatures?

No! Most systems, including a classical gas (e.g. the air around us), are limited to positive absolute temperatures.
In order to be able to reach negative temperatures, a system needs to possess an upper bound for the energy of its particles, i.e. a maximal possible energy a particle of the system can have.
This limit is not an external limit in the sense that there is just no more energy available. It is an internal limit - the particles cannot absorb more energy even if there is plenty available. Atoms in a classical gas, for example, do not possess such an upper energy limit - their kinetic energy can be arbitrarily high. Even the speed of light as the ultimate speed limit for particles does not pose a limit to their kinetic energy: Although the speed of the particles is limited by the speed of light, the kinetic energy can still be arbitrarily high.
In fact, the idea of negative absolute temperature is old, but was seldom discussed for mobile particles because everybody assumed that it was impossible to realize.

Is your system really colder than zero Kelvin?

No! Nothing can be colder than absolute zero (0K)!
Negative absolute temperatures (or negative Kelvin temperatures) are hotter than all positive temperatures - even hotter than infinite temperature.

What does hotter or colder actually mean?

Take two glasses of water, one with hot water and one with cold water. If you mix the water, you will get medium hot water. In the language of thermodynamics, this means that heat was transferred from the hot water to the cold water, until they both reached the same temperature.
So heat always flows from the hotter to the colder system.
And since negative temperature systems have a lot of energy, heat will flow from negative temperature systems to positive temperature systems.

Did you redefine temperature?

No. We use the textbook definition of temperature.

How is temperature formally defined?

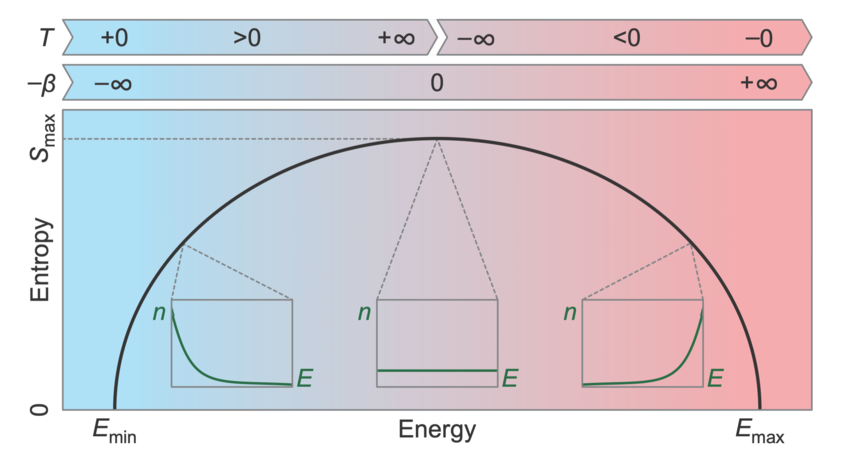
Temperature is defined via entropy: The inverse of temperature (1/T) is defined as the change of entropy (S) in a system, when the total energy E of the system is changed: 1/T=∂S/∂E.
Total energy is the sum of the energy of all particles of the system, and entropy is explained later in this FAQ. Below we show a typical curve of entropy versus energy in a system that has a minimum (E_min) and maximum (E_max) energy. The slope of this curve indicates how entropy changes with energy, ∂S/∂E, and therefore gives the inverse temperature, 1/T.

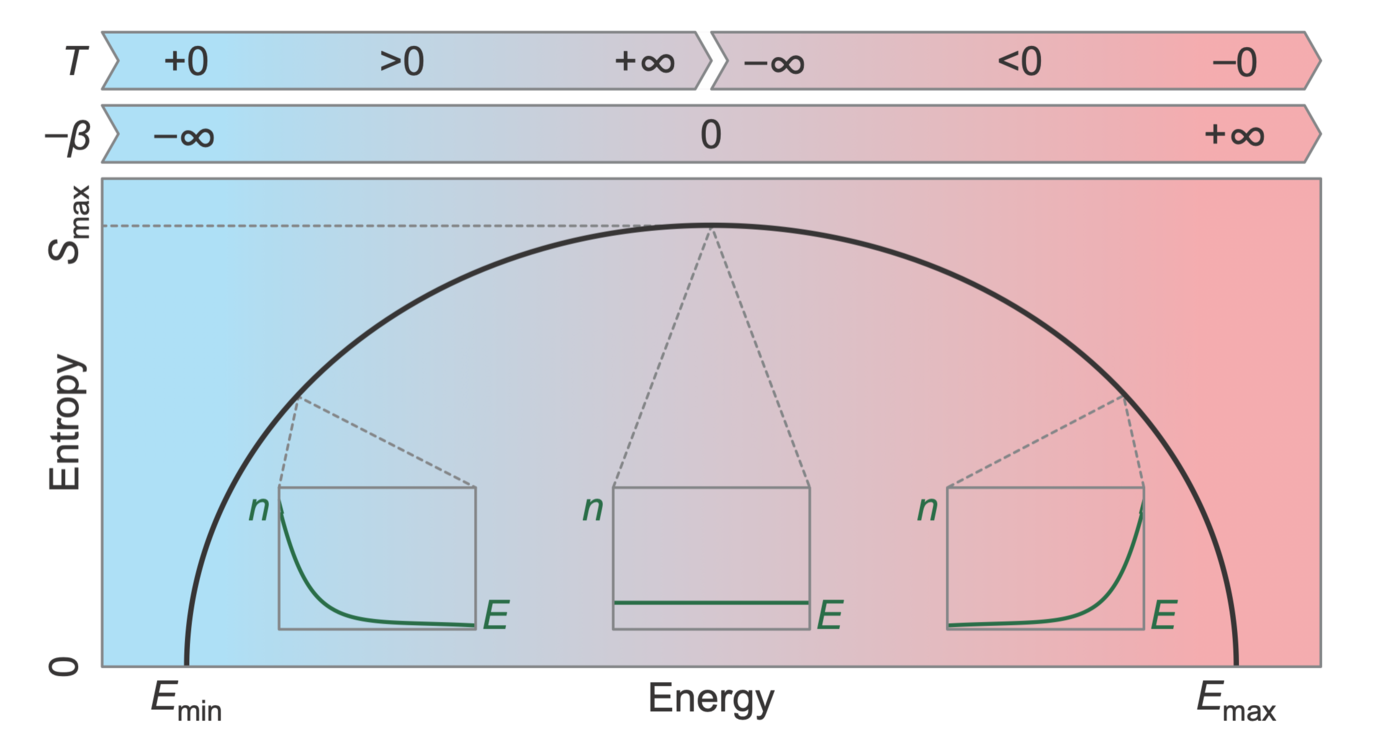
Definition of temperature: If the energy in the system is minimal (Emin), all particles are in the lowest possible energy state and the entropy is zero. The curve is vertical at this point with an infinite slope and temperature is therefore zero. If the energy increases, the particles begin to occupy higher energy states, and the entropy increases. There are, however, always more particles at low energies than at high energies – the usual Boltzmann distribution (see green curve). The slope of the entropy versus energy curve decreases and the temperature therefore increases. At some point, when there is enough energy in the system, the particles distribute equally over all energy states. The disorder and therefore also the entropy are maximal (Smax). The curve is completely flat at this point, with a slope of zero, and the temperature is therefore infinite. If the total energy in the system is further increased, more particles will occupy high energies than low energies – the Boltzmann distribution will be inverted. Because the energy distribution becomes narrower again, disorder and thereby entropy start to decrease. This is a very unusual behavior – usually entropy increases with increasing energy. The slope of the curve is negative in this regime and therefore also the absolute temperature is negative. If the energy in the system is maximal (Emax), all particles are at their maximum possible energy. The entropy is zero again. The curve is again vertical, therefore the temperature is zero again, but this time coming from negative values. Thus, while a temperature of positive and negative infinity is physically identical, temperatures of positive and negative zero are very different. The jump in temperature from positive to negative infinity is a consequence of the historic definition of temperature. If temperature was defined differently, for example as -β=-1/T as shown in the second line, there would not be such a discontinuity. — Definition of temperature: If the energy in the system is minimal (E_min), all particles are in the lowest possible energy state and the entropy is zero. The curve is vertical at this point with an infinite slope and temperature is therefore zero. If the energy increases, the particles begin to occupy higher energy states, and the entropy increases. There are, however, always more particles at low energies than at high energies – the usual Boltzmann distribution (see green curve). The slope of the entropy versus energy curve decreases and the temperature therefore increases. At some point, when there is enough energy in the system, the particles distribute equally over all energy states. The disorder and therefore also the entropy are maximal (S_max). The curve is completely flat at this point, with a slope of zero, and the temperature is therefore infinite. If the total energy in the system is further increased, more particles will occupy high energies than low energies – the Boltzmann distribution will be inverted. Because the energy distribution becomes narrower again, disorder and thereby entropy start to decrease. This is a very unusual behavior – usually entropy increases with increasing energy. The slope of the curve is negative in this regime and therefore also the absolute temperature is negative. If the energy in the system is maximal (E_max), all particles are at their maximum possible energy. The entropy is zero again. The curve is again vertical, therefore the temperature is zero again, but this time coming from negative values. Thus, while a temperature of positive and negative infinity is physically identical, temperatures of positive and negative zero are very different. The jump in temperature from positive to negative infinity is a consequence of the historic definition of temperature. If temperature was defined differently, for example as -β=-1/T as shown in the second line, there would not be such a discontinuity.

Definition of temperature: If the energy in the system is minimal (E_min), all particles are in the lowest possible energy state and the entropy is zero. The curve is vertical at this point with an infinite slope and temperature is therefore zero. If the energy increases, the particles begin to occupy higher energy states, and the entropy increases. There are, however, always more particles at low energies than at high energies – the usual Boltzmann distribution (see green curve). The slope of the entropy versus energy curve decreases and the temperature therefore increases. At some point, when there is enough energy in the system, the particles distribute equally over all energy states. The disorder and therefore also the entropy are maximal (S_max). The curve is completely flat at this point, with a slope of zero, and the temperature is therefore infinite. If the total energy in the system is further increased, more particles will occupy high energies than low energies – the Boltzmann distribution will be inverted. Because the energy distribution becomes narrower again, disorder and thereby entropy start to decrease. This is a very unusual behavior – usually entropy increases with increasing energy. The slope of the curve is negative in this regime and therefore also the absolute temperature is negative. If the energy in the system is maximal (E_max), all particles are at their maximum possible energy. The entropy is zero again. The curve is again vertical, therefore the temperature is zero again, but this time coming from negative values.
Thus, while a temperature of positive and negative infinity is physically identical, temperatures of positive and negative zero are very different.
The jump in temperature from positive to negative infinity is a consequence of the historic definition of temperature. If temperature was defined differently, for example as -β=-1/T as shown in the second line, there would not be such a discontinuity.

What is entropy and how is it related to temperature?

Entropy is a measure of disorder in the system.
It is related to the number of energy states that are occupied by the particles: If only one energy state is occupied, as for example the lowest energy state in the case of a temperature of zero Kelvin, the system is very ordered and the entropy is zero. If the particles are however distributed over many energy states, low energy and high energy, the system is very disordered and the entropy is large. Temperature is defined via entropy – see above.

What does temperature actually mean?

In a classical gas - think of many independent billiard balls - temperature describes how the particles are distributed among their possible states, for instance their velocities. As these states can have different energies, this means that in such a gas all atoms together have one particular temperature, but the individual atoms do not have the same energy.
The distribution of energies is called the Boltzmann distribution and describes the following: At absolute zero (plus zero), all particles are at rest and their kinetic energy is zero. So the distribution of energies has a sharp peak at zero - here are all the atoms - and is zero otherwise. If you now heat up the gas, you increase both its temperature and its total energy and this sharp peak will broaden (see the left inset in the above figure). So you can find some atoms now at higher energies. But you will still find more atoms at a state with lower energy than at a state with higher energy. The hotter the gas becomes, the broader and shallower this peak becomes, until at infinite temperature the distribution would be completely flat and all states would be equally probable (middle inset).
Negative temperature now means that this distribution is inverted or flipped around, so that you find more atoms in a higher energy state than in a lower one (right inset). This means that the peak in the distribution is not at the lowest energy anymore, but at the highest possible energy.
In general, the thermal distribution does not only take kinetic energy into account, but all forms of energy that the particles can possess, for example potential energy or magnetic energy.

How do you measure temperature? Do you put a thermometer close to the atoms?

Measuring temperature is indeed a difficult task. Unfortunately, we cannot put a thermometer into our system, close to the atoms.
Instead, we take images of our atoms with a CCD camera. These images show us the distribution of atoms. For each temperature, we theoretically expect a certain distribution. We compare the distribution of our atoms with the theoretically expected distributions. The distribution that fits best gives us the temperature of the atoms.

Do your atoms really have negative absolute temperature or do they just behave like that?

Our atoms really have negative absolute temperature!
The way temperature is defined tells us the following: If a system thermalizes, i.e. tries to reach thermal equilibrium, and if we can describe the distribution of the system with some Boltzmann distribution, and if this distribution remains stable over some time, we know that the system has reached thermal equilibrium. We can then assign the corresponding temperature to the system. The system then really has this temperature. In our case, as the Boltzmann distribution of our atoms is inverted, this temperature is negative.

How should I think about the temperature axis? I always thought it goes from zero to infinity.

For most systems (like the classical gas) this is correct, as these systems cannot have negative absolute temperatures. For those systems that can assume negative temperatures, the temperature scale also starts at plus zero, increases until infinity, then jumps to minus infinity and increases further until minus zero.

Does that mean that temperature is circular?

No! Plus zero and minus zero are not connected in this case, in fact they are as far away as possible.
Think of the ordinary line of reals numbers: It starts at minus infinity, runs through zero, and goes to plus infinity. Now imagine cutting this line at zero into two parts. You end up with two lines, one running from minus infinity to zero, this end is called minus zero; and a second part running from plus zero to plus infinity. Now we glue the two ends at plus and minus infinity together and pull the two loose ends at the zeros apart. So we end with a line like this:
+0,...,+10,...,+infinity,-infinity,...,-10,...,-0
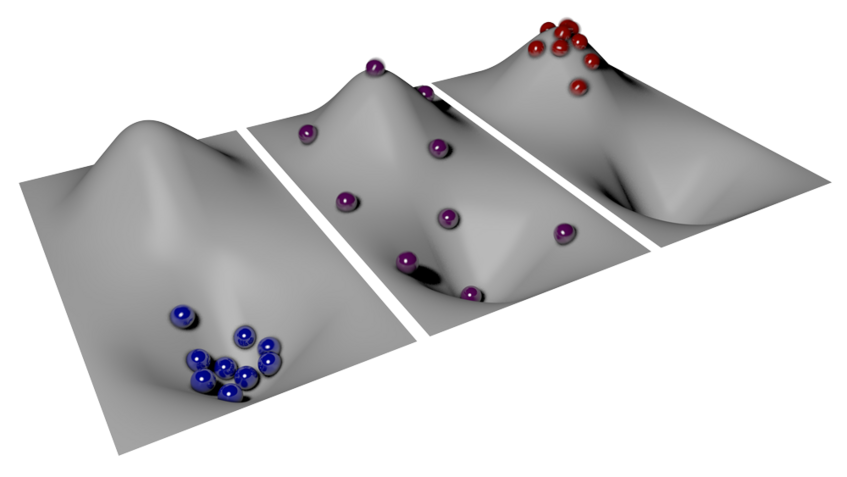
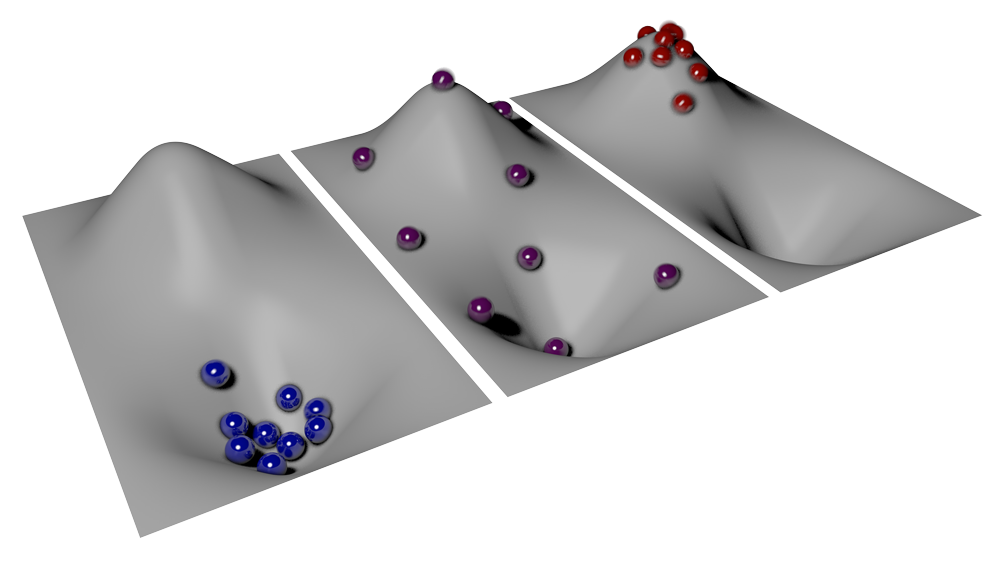
So the two zeros are as far apart as possible, in fact plus zero corresponds to the state where all particles are in the lowest energy state (the bottom of the valley in the picture below) while minus zero corresponds to the state that all particles are in the state with the highest possible energy (the top of the hill).

Temperature in a game of marbles

The thermal distribution (or Boltzmann distribution) can be illustrated with balls that are distributed on a hilly landscape, where the altitude symbolizes the energy of the balls. At positive temperatures (left figure), as they are common in everyday life, most balls lie in the valley around minimum energy. This illustrates that states with small total energy are more likely than those with large total energy – the usual Boltzmann distribution. At plus or minus infinite temperature (central figure) the balls spread evenly over low and high energies in an identical landscape. Here, all energy states are equally probable. At negative temperatures (right figure), however, most balls can be found on top of the hill, at the upper limit of possible energies. Energy states with large total energy are occupied more than those with small total energy – the Boltzmann distribution is inverted.

The thermal distribution (or Boltzmann distribution) can be illustrated with balls that are distributed on a hilly landscape, where the altitude symbolizes the energy of the balls. At positive temperatures (left figure), as they are common in everyday life, most balls lie in the valley around minimum energy. This illustrates that states with small total energy are more likely than those with large total energy – the usual Boltzmann distribution. At plus or minus infinite temperature (central figure) the balls spread evenly over low and high energies in an identical landscape. Here, all energy states are equally probable. At negative temperatures (right figure), however, most balls can be found on top of the hill, at the upper limit of possible energies. Energy states with large total energy are occupied more than those with small total energy – the Boltzmann distribution is inverted.

Why do you need an upper limit in energy for a negative temperature state but not for a positive temperature one?

The situation is in fact completely symmetric: You need a lower bound for the energy in order to get positive temperatures and an upper bound in order to get negative temperatures.
The most intuitive way to see this is by considering the picture of the valley and the hill: At small positive temperatures you will find most marbles close to the lowest point, near the floor of the valley, which represents the lower bound in energy. If there would not be such a bound, there would be an infinitely deep hole instead and all marbles would continue to fall down the hole without ever reaching a stable state. For negative temperatures, where all particles want to pile up on top of the mountain, we similarly require that the mountain has a finite height.
For the classical picture of free moving particles, kinetic energy obviously has a lower bound - the particles stand still - so that we rarely need to think about this requirement.

How can plus infinity and minus infinity be the same thing?

In statistical mechanics the temperature T is not used that often. Most times we use β, which is the inverse: β=1/T. Concerning β, plus infinite temperature and minus infinite temperature are the same, namely zero. In fact, -β would have been a better choice for the definition of temperature, as it runs from minus infinity via zero to plus infinity, thereby avoiding the jump from plus to minus infinity and the confusion with "hot negative absolute temperatures". (see also "How is temperature formally defined?")

Are the atoms really stable at negative absolute temperature or do you just hold the atoms in place, at maximum energy?

The atoms at negative absolute temperature are really stable by themselves!
We create the system with several laser beams and a magnetic field in a vacuum chamber. This altogether constitutes the environment in which the atoms "live", a world with bright and dark regions in which the atoms are trapped. Once the atoms are prepared at negative absolute temperature, with many atoms close to maximum energy, they stay there. They stay there just as long as atoms at positive absolute temperature in a comparable system which are mainly sitting at minimum energy.
This can be illustrated with the landscape above. At positive temperature, most marbles lie in the valley. This state is stable - this is nature as we know it. If marbles lie on top of the hill they will usually roll down the hill and thereby convert potential energy into kinetic energy. If these marbles are, however, at negative absolute temperature, all their energy forms will be close to their maximum allowed values. In the picture this is apparently true for potential energy, as the marbles lie on top of the hill, the highest point in the landscape. But it is also true for kinetic energy: The marbles on top of the hill move around fast. Because kinetic energy cannot increase further, the marbles cannot convert potential energy into kinetic energy. Therefore they cannot roll down at all. They stay on top of the hill - the system is stable.

Shouldn't the atoms at negative absolute temperature that are hotter than infinity burn away your lab?

No. The crucial point to consider here is the amount of energy that is contained in a system.
Our atoms are very hot in the sense that they contain a lot of energy: The energy of most atoms is close to the maximum that is allowed by the upper limit for their energy. This maximum energy, however, is very little compared to, for example, the kinetic energy of a typical water molecule in a pot of water at room temperature. Additionally, our system at negative absolute temperature consists only of around a hundred thousand atoms. This is about 17 orders of magnitude less than the number of water molecules in only a milliliter of water. If you sum up the energy of all our atoms, the total energy contained in our system at negative absolute temperature is therefore very small compared to energies that we are used to in everyday life.
It is definitely easier to harm yourself with a pot of boiling water. Although water is not at negative absolute temperature, but "only" at positive absolute temperature, the total energy contained in the pot will be much higher than in our system. If you dip your finger into the hot water, a lot of energy will be transferred to your finger, and that hurts. If you could, however, dip your finger into our system, only very little energy would be transferred.

Where do you get your upper limit for kinetic energy from?

We put our atoms into a so-called optical lattice that consists of a periodic potential created by interfering laser beams. For our atoms, this periodic potential acts in the same way as the potential formed by the ions in a solid acts for the electrons - it creates a band structure.
This means that, due to this potential, the kinetic energy splits up into different bands, e.g. valence and conduction band in a metal or semi-conductor. These bands are separated in energy by so-called band gaps - regions of energy without any states for the particles. Therefore, each band naturally possesses a lower as well as an upper bound for the kinetic energy. We put all our atoms into one of these bands and therefore created the required upper bound for the kinetic energy.
This on its own is nowadays done routinely in many labs. The new ingredient in our work is that we also created upper limits for the interaction energy and the potential energy. The latter, for example, we limited by transforming the optical trap, in which the atoms sit, into an anti-trap, i.e. transforming a valley into a hill.

Do lasers also have a negative absolute temperature?

No! A temperature can only be assigned to a state in thermal equilibrium. This means states that, when left alone (when the system is thermally isolated) will remain stable and do not change over time. The particles in a laser medium do have an inverted energy population -more particles are in excited states than in low energy states- and their distribution looks indeed similar to a state at negative temperature. This inverted energy population, however, only exists as long as the laser is continuously pumped, i.e. particles are actively pumped into the exited states. When you switch-off the pump, all atoms will decay back into the lower state and their energy goes into the laser beam. So, while pumped, the laser medium is in a steady state, but not in a thermal state. It is not in thermal equilibrium and therefore cannot have a temperature.

What is this possible connection to cosmology?

We could show that our atomic system is stable, even though the atoms strongly attract each other - that means they want to collapse but cannot due to being at negative temperature.
And the universe as a whole is also not collapsing under the attractive force of gravity - on the contrary, its expansion is accelerating. In cosmology, dark energy is introduced exactly to describe this effect.
But whether this hints at some connection or is just a coincidence remains to be seen.